从零开始刷一下leetcode非会员题(尽量使用最优算法)
Week1
暴力枚举可过,时间复杂度O(n2)
哈希表:思路为遍历数组,判断当前元素前有无元素与其之和等于target,而哈希表查找元素的时间复杂度为O(1),我们可以每当遍历一个元素而找不到与其之和满足要求的元素时,将其存入哈希表以便后续查找,这样即可将算法总时间复杂度优化到O(n)
tips:C++语法中自带两个哈希表数据结构,分别为有序map(底层为红黑树实现),查找时间复杂度为log2n,而无序哈希表unordered_map时间复杂度为O(1),本题用后者
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> res;
unordered_map<int,int> hash;
for(int i=0;i<nums.size();i++)
{
int r=target-nums[i];
if(hash.count(r))
{
res.push_back(hash[r]);
res.push_back(i);
}
hash[nums[i]]=i;
}
return res;
}
};
|
示例:
1
2
3
| 输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
|
给出数据以链表形式倒序存储,从个位依次运算即可(注意细节)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* Newhead=new ListNode(-1);
ListNode* cur=Newhead;
int t=0;
while(l1||l2||t)
{
if(l1)
{
t+=l1->val;
l1=l1->next;
}
if(l2)
{
t+=l2->val;
l2=l2->next;
}
cur->next=new ListNode(t%10);
t/=10;
cur=cur->next;
}
return Newhead->next;
}
};
|
初见可能比较难,先了解一下双指针算法和滑动窗口算法
基本思路:要找出给定字符串s中不含重复字符的最长子串。基本思路肯定是遍历所有子串,并找出符合条件的。我们以字串尾字符为基准进行遍历,若暴力遍历时间复杂度为O(n2)
优化办法:假设尾节点为j时,无重复字符最长子串头节点为i,当我们遍历尾节点为j+1的所有子串时,满足条件的头节点i′仅可能出现在i或其右侧,这样使两个指针遍历时“不走回头路”,类似滑动窗口,可将算法时间复杂度优化至O(n)
其他细节:我们可以用哈希表来维护指针i、j之间元素出现的个数,便于判断其间有无重复元素,每次i指针向前移动一次,将其存入哈希表,若有重复元素则定为i指向元素值,j向前移动至该元素仅出现一次即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<char,int> hash;
int i=0;
int res=0;
for(int j=0;j<s.size();j++)
{
hash[s[j]]++;
while(hash[s[j]]>1)
{
hash[s[i++]]--;
}
res=max(res,j-i+1);
}
return res;
}
};
|
中位数:有序数组元素个数为奇数时,中位数为最中间的数,若元素个数为偶数时,中位数为中间两个数的平均数
朴素算法:将两个数组合并,sort排序后遍历寻找中位数,时间复杂度为O(nlogn),不满足题目要求
优化:本质上我们需要找到两数组排序后第k=2m+n)小的数,我们可以从题目要求的时间复杂度入手O(log(m+n)),尝试二分的思想。
(若A、B数组的元素个数均大于2k时)各取A、B数组中第2k个元素,若A中所取元素小于B中所取元素,即A中元素取少了,B中元素取多了,则A中前2k个元素必定在要取中位数前(换句话说中位数不可能出现在这些元素中),我们可以不再考虑这些元素。反之也成立,由此可将k的规模减少一半,在剩下的数据中寻找第k−2k小的元素,将其作为新的k值继续递归即可。
(若A、B数组的元素个数有一个小于2k时,不可能全部小于)那取小数组的最后一个元素与大数组的2k个元素,若前者小于后者,则中位数不可能出在前一个数组中,即中位数为大数组的第k−m个数,若后者小于前者,则后数组前2k个元素中不存在中位数。删去前2k个元素即可。
时间复杂度:k=2m+n),每次递归k的规模减小一半,则时间复杂度为O(log(m+n))
注意:考虑数组越界问题,find()函数实现时确保前一个数组一定小于后一个数组,这样可以避免很多边界问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int total=nums1.size()+nums2.size();
if(total%2==0)
{
int left=findknumber(nums1,0,nums2,0,total/2);
int right=findknumber(nums1,0,nums2,0,total/2+1);
return (left+right)/2.0;
}
else return findknumber(nums1,0,nums2,0,total/2+1);
}
int findknumber(vector<int>& nums1, int i, vector<int>& nums2, int j,int k)
{
if(nums1.size()-i>nums2.size()-j) return findknumber(nums2,j,nums1,i,k);
if(nums1.size()==i) return nums2[j-1+k];
if(k==1) return min(nums1[i],nums2[j]);
int si=min(i+k/2,int(nums1.size()));
int sj=j+k/2;
if(nums1[si-1]>nums2[sj-1])
{
return findknumber(nums1,i,nums2,sj,k-(sj-j));
}
else
{
return findknumber(nums1,si,nums2,j,k-(si-i));
}
}
};
|
有一种利用二分非递归的做法,可将时间复杂度优化到O(log(min(m,n))),但细节处较为繁琐,待我学学再做补充
经典题目,做法很多,有Manacher算法时间复杂度可优化到O(n),但该算法几乎只可解决此类问题,并不实用,字符串哈希搭配二分O(nlogn)(以后补充)
因为该题给出的数据量较小,此处我们选择一种便于理解的O(n2)的算法,此题用DP也可过但需要额外的空间复杂度
基本思路:回文串指左右对称的字符串,大体分为奇数型和偶数型,遍历整个字符串,选取中间节点i,若为奇数型,从[i−1,i+1] 向左右寻找,直到遇到不同字符或数组边界,若为偶数型,从[i,i+1] 向左右寻找即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
string longestPalindrome(string s) {
string res;
for(int i=0;i<s.size();i++)
{
int l=i-1;
int r=i+1;
while(l>=0 && r<=s.size() && s[l]==s[r])
{
l--;
r++;
}
if(res.size()<r-l-1) res=s.substr(l+1,r-l-1);
l=i;
r=i+1;
while(l>=0 && r<=s.size() && s[l]==s[r])
{
l--;
r++;
}
if(res.size()<r-l-1) res=s.substr(l+1,r-l-1);
}
return res;
}
};
|
样例:s=PAYPALISHIRING numRows=3
1
2
3
4
5
| P A H N
A P L S I I G
Y I R
# PAHNAPLSIIGYIR
|
本质即为找规律,第一行和最后一行可看成一个等差数列,中间行可看为两个等差数列,注意首项和公差之间的规律即可(注意当n==1,公差为0会进入死循环,需要特殊判断)
1
2
3
4
5
6
| 1 11 21 31
2 10 12 20 22 30 32
3 9 13 19 23 29 33
4 8 14 18 24 28 34
5 7 15 17 25 27 35
6 16 26 36
|
以数字字符串为例,便于找到规律。所有等差数列公差为2n−2,除第一行与最后一行,两等差数列首项之差为2n−2−i(i为行头元素)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
string convert(string s, int numRows) {
string res;
if(numRows==1) return s;
for(int i=0;i<numRows;i++)
{
if(i==0||i==numRows-1)
{
for(int j=i;j<s.size();j+=2*numRows-2)
{
res+=s[j];
}
}
else
{
for(int j=i,k=2*numRows-2-i;j<s.size()||k<s.size();j+=2*numRows-2,k+=2*numRows-2)
{
if(j<s.size()) res+=s[j];
if(k<s.size()) res+=s[k];
}
}
}
return res;
}
};
|
注意题目要求:如果反转后整数超过 32 位的有符号整数的范围 [−231,231−1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。即不使用longlong类型存放数据
将数据存入字符串中,用字符串内置方法可过,这里用数学方法
基本思路:思路非常简单,每次通过模10运算取出最后一位与上次保留结果的十倍相加(秦九韶算法),此方法对负数依然成立,根本原因为C++中的取模运算与数学中不同,负数取模仍返回负数,这对我们的算法有利
不限制longlong型:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
int reverse(int x) {
long long r=0;
while(x)
{
r=r*10+x%10;
x /= 10;
}
if(r>INT_MAX) return 0;
if(r<INT_MIN) return 0;
return r;
}
};
|
如果限制只能使用int类型存储的话,我们要再循环内判断是否超过范围。假设r为正数时,想判断10*r+x%10>INT_MAX,直接判断会爆int,我们根据数学方法变形为r>((INT_MAX-x%10))/10即可,负数同理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
int reverse(int x) {
int r=0;
while(x)
{
if(r>0&&r>(INT_MAX-x%10)/10) return 0;
if(r<0&&r<(INT_MIN-x%10)/10) return 0;
r=r*10+x%10;
x /= 10;
}
return r;
}
};
|
典型的模拟题,需要自己模拟atoi函数,这题要求很多,按需求一步一步来
思路比较常规,和上一题一样(秦九韶算法),一位位读取即可
不限制long long类型的写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
int myAtoi(string s) {
int k=0;
while(k<s.size()&&s[k]==' ') k++;
if(k==s.size()) return 0;
int minus =1;
if(s[k]=='-')
{
minus=-1;
k++;
}
else if(s[k]=='+') k++;
long long res=0;
while(k<s.size()&&s[k]>='0'&&s[k]<='9')
{
res=res*10+(s[k]-'0');
k++;
if(res>INT_MAX) break;
}
res *= minus;
if(res>INT_MAX) return INT_MAX;
if(res<INT_MIN) return INT_MIN;
return res;
}
};
|
如果限制只能使用int类型,我们只需要在存数时改变越界的判断即可,这里有一个坑点,在while循环中我们存放的是整数的绝对值,而int类型的最小值为-2147483648,最大值为2147483647,这就导致恰好为最小值时我们无法将其绝对值存入,需要特殊判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
int myAtoi(string s) {
int k=0;
while(k<s.size()&&s[k]==' ') k++;
if(k==s.size()) return 0;
int minus =1;
if(s[k]=='-')
{
minus=-1;
k++;
}
else if(s[k]=='+') k++;
int res=0;
while(k<s.size()&&s[k]>='0'&&s[k]<='9')
{
if(minus>0&&res>(INT_MAX-(s[k]-'0'))/10) return INT_MAX;
if(minus<0&&-res<(INT_MIN+(s[k]-'0'))/10) return INT_MIN;
if(-res*10-(s[k]-'0')==INT_MIN) return INT_MIN;
res=res*10+(s[k]-'0');
k++;
}
res *= minus;
return res;
}
};
|
简单题做法很多
转换成字符串:看反转后与之前是否相同(rbegin()、rend()反向迭代器)
1
2
3
4
5
6
7
| class Solution {
public:
bool isPalindrome(int x) {
string s=to_string(x);
return s==string(s.rbegin(),s.rend());
}
};
|
或者可以用第七题中整数反转思想反转(负数可直接特判为false)
很喜欢一条评论——这不仅是我刷的第十道题,也是我人生中的一道坎
这种两个字符串匹配的问题通常可以使用DP(动态规划来解决),我们来分析一下,两个字符串的DP问题我们通常用二维数组存储
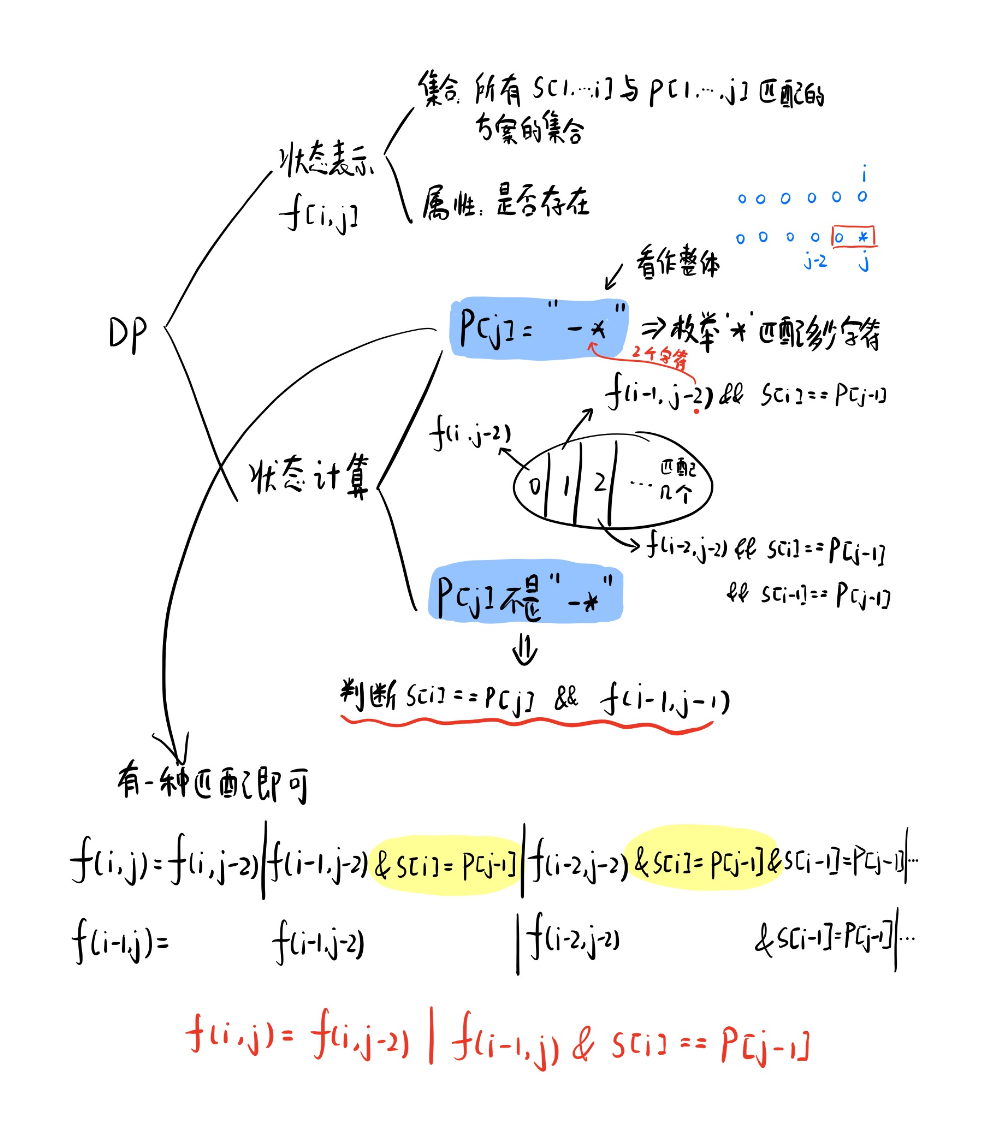
注意:本题中*代表匹配零个或多个前面的那一个元素,和正常的正则语法不同,这里看了半天😈
时间复杂度分析:这里按照图中黑字的状态转移方程,更新状态时间复杂度为O(n2),枚举*匹配的字符个数时间复杂度为O(n),总时间复杂度为O(n3),需要进行优化
我们可以列出f(i-1,j)的状态转移方程,发现其中的共用部分,用其状态来更新f(i,j)的状态,可将枚举阶段的时间复杂度优化为O(n),最终状态方程如以上红字(优化方式类似于完全背包)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
bool isMatch(string s, string p) {
int n = s.size(), m = p.size();
s = ' ' + s, p = ' ' + p;
vector<vector<bool>> f(n + 1, vector<bool> (m + 1));
f[0][0] = true;
for (int i = 0; i <= n; i ++)
for (int j = 1; j <= m; j ++)
{
if (i && p[j] != '*')
{
f[i][j] = f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.');
}
else if (p[j] == '*')
{
f[i][j] = f[i][j - 2] ||(i && f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '.'));
}
}
return f[n][m];
}
};
|
Week2
这道题没找到合适的算法可以解决orz,暴力遍历时间复杂度O(n2),看了大佬的题解可以用单调栈+二分达到O(nlogn)。(还不会以后补过)
不妨从数学角度理解(贪心),找到盛水容器的最优解,先说结论,利用双指针扫描数组,i、j分别指向数组的首尾,若左边界的高度大于右边界,则j--,反之则i++,直到两指针相遇,每次迭代更新最大值,即可找到最优解,时间复杂度可优化到O(n)(思路较为巧妙,建议背过)
难点在于证明该做法的正误:在指针逼近的过程中,必定出现一边指针先到达最优解边界的情况,这里假设左边界先到达,此时预期最优解的边界坐标小于当前右指针j。利用反证法,假设左边界高度小于等于右边界高度,预期解的容水量必定小于当前,矛盾,故左边界的高度大于右边界,右指针左移,必定能得到最优解

1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public:
int maxArea(vector<int>& height) {
int res=0;
for(int i=0,j=height.size()-1;i<j;)
{
res=max(min(height[i],height[j])*(j-i),res);
if(height[i]<height[j]) i++;
else j--;
}
return res;
}
};
|
水题,因为数据量仅为1-3999,打表都能过,为了显得不那么业余,浅找一下规律
1
2
3
4
| 1 ->I 4 ->IV 5 ->V 9 ->IX
10->X 40->XL 50->L 90->XC
100->C 400->CD 500->D 900->CM
1000->M
|
记录一下特殊情况,若大于特殊值在后面补I、X、C、M即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
string intToRoman(int num) {
int values[]={
1000,
900,500,400,100,
90,50,40,10,
9,5,4,1
};
string str[]={
"M",
"CM","D","CD","C",
"XC","L","XL","X",
"IX","V","IV","I"
};
string result;
for(int i=0;i<13;i++)
{
while(num>=values[i])
{
num-=values[i];
result+=str[i];
}
}
return result;
}
};
|
是上一题的逆运算,直接将各罗马数字的值相加即可,注意要特殊判断如果前面的罗马数字代表的值小于后面,要减去前面罗马数字的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public:
int romanToInt(string s) {
unordered_map<char,int> hash;
hash['I']=1;
hash['V']=5;
hash['X']=10;
hash['L']=50;
hash['C']=100;
hash['D']=500;
hash['M']=1000;
int res=0;
for(int i=0;i<s.size();i++)
{
if(i+1<s.size() && hash[s[i]]<hash[s[i+1]])
res-=hash[s[i]];
else
res+=hash[s[i]];
}
return res;
}
};
|
简单题,就是循环枚举每个字符串的每个字母,直到前缀超过某一字符串的长度或有字母不匹配输出结果即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
string res;
if(!strs.size()) return res;
for(int i=0;;i++){
if(i>=strs[0].size()) return res;
char ch=strs[0][i];
for(int j=1;j<strs.size();j++){
if(i>=strs[j].size()||ch!=strs[j][i])
return res;
}
res+=ch;
}
}
};
|
双指针算法,要求数组有序所以先排序,假设指针i、j、k指向的值依次增大,枚举i的位置,j、k指针使用双指针算法,暴力遍历时间复杂度为O(n2) ,找到第一个j指针位置和其对应的k指针,使得刚好满足num[i]+num[j]+num[k]>=0,因为有序,j向前遍历,k指针只能向后寻找,将时间复杂度优化为O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> res;
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size();i++)
{
if(i&&nums[i]==nums[i-1]) continue;
for(int j=i+1,k=nums.size()-1;j<k;j++)
{
if(j>i+1&&nums[j]==nums[j-1]) continue;
while(j<k-1&&nums[i]+nums[j]+nums[k-1]>=0) k--;
if(nums[i]+nums[j]+nums[k]==0)
{
res.push_back({nums[i],nums[j],nums[k]});
}
}
}
return res;
}
};
|








